 |
[2]False eyes

· As we have seen, a group dies if it doesn't have two eyes. You have to have two certain eyes, but there is a confusing position in which you have a false eye that is not a proper eye. Let's learn how to distinguish between perfect eyes and false eyes.
(a)'Undecided eyes' and 'false eyes'
· Dia. 36. The black group has not yet made two definite eyes. The X point is a perfect eye, but the 'a' point is still undecided. If Black plays first, he can make a perfect eye, so he lives, but if White plays first, it becomes a false eye, so the group dies. |
 |

Dia. 36 |
|
Dia. 37. If Black plays 1, the 'a' point becomes a perfect eye. Black lives with two eyes, so White can't do anything. |
 |

Dia. 37 |
|
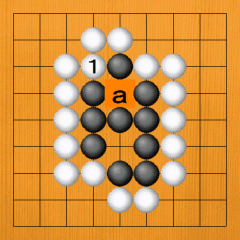
Dia. 38. However, if White plays first, White 1 makes the 'a' point a false eye. |
 |
Dia. 38 |
|
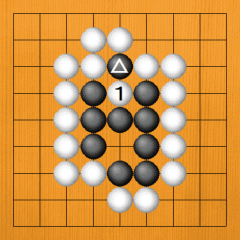
Dia. 39. The marked black stone is surrounded on three sides, so White can capture it by playing at 1. |
 |
Dia. 39 |
|
Dia. 40. Even if Black saves the stone by connecting at 1, he can't make an eye here. The whole group has only one vacant point, at X, so this group is dead. A false eye doesn't have the value of a real eye. |
 |

Dia. 40 |
|
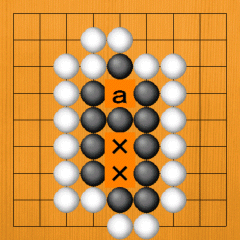
Dia. 41. Even if Black has two vacant X points, the 'a' point is a false eye, so it's the same thing. Sooner or later, the 'a' point will be filled. This group can't make two eyes. |
 |
Dia. 41 |
|
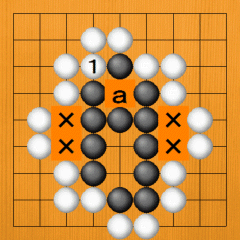
· Dia. 42. The white group that is surrounding Black is not all in contact withBlack. The X points are open, so Black is not tightly sealed in. However, Black can't make eyes on these points, and escaping to the outside is impossible. If White plays at 1, the 'a' point becomes a false eye, so Black can't live. |
 |
Dia. 42 |
|
Dia. 43. The X point is open, but 'a' is an undecided eye in the same way. |
 |
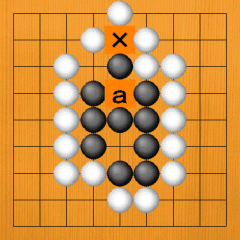
Dia. 43 |
|
Dia. 44. If it is Black's turn, he can play at 1 and make two eyes, but not if it is White's turn to play. |
 |

Dia. 44 |
|
Dia. 45. If White plays at 1, the 'a' point becomes a false eye. |
 |
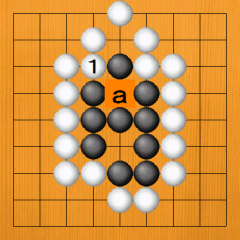
Dia. 45 |
(b) Two false eyes
· Dia. 46. The black group has three points that look like eyes. The X point is a perfect eye, but 'a' and 'b' are undecided eyes. In this case, securing one of these points as a perfect eye is good enough, so this group is alive as it stands. |
 |
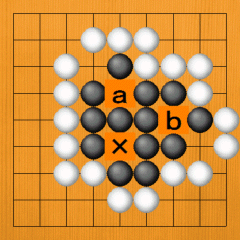
Dia. 46 |
|
Dia. 47. Even if White makes one of these eyes a false one with 1, Black can make a perfect eye with 2, so he gets two eyes. |
 |
Dia. 47
|
(e) Three false eyes
· What happens if you don't have one perfect eye, but you have three undecided eyes? In Dia. 48, Black has only three undecided eyes, but he can live if it is his turn. |
 |

Dia. 48 |
|
· Dia. 49. If Black plays at 1 and secures one perfect eye, he can make two eyes. Even if White makes one of the undecided eyes a false eye with 2, Black can turn the other into a perfect eye with 3, so he lives with two eyes. |
 |
Dia. 49
|
|
Dia. 50. If it is White's turn to play, Black dies. White first makes one of the undecided eyes a false eye with 1. Even if Black makes one perfect eye with 2, White makes the remaining one a false eye with 3. Overall, the black group can make only one eye, so Black dies when it's White's turn. |
 |
Dia. 50
|
· (Application 1)
· Our theme is understanding the true nature of false eyes. In Dia. 51, the black eye below is a perfect eye, but what about the two X points above? If you understand this, you can graduate from the course in false eyes. |
 |
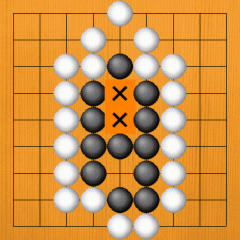
Dia. 51 |
|
Dia. 52. First, let's look at it from Black's point of view. If Black plays at 1, the X point becomes a perfect eye. Added to the eye below, this makes two eyes, so Black is alive. |
 |
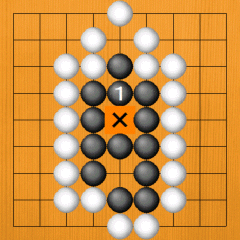
Dia. 52 |
|
· Well, what if it is White's turn? If White plays on the outside at 1 in Dia. 53, Black connects at 2. The X point becomes a perfect eye, so the group is alive. White 1 is a mistake. |
 |
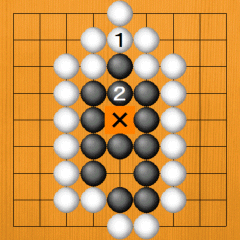
Dia. 53 |
|
Dia. 54. If White plays inside at 1, this becomes a false eye. Next, even if Black captures at 2 -->
|
 |
Dia. 54
|
|
Dia. 55. The X point is a false eye. Having come this far, we can see that the black group is not alive. |
 |
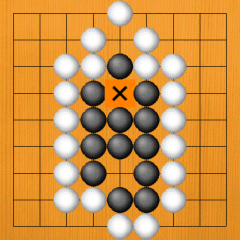
Dia. 55 |
|
 |